| |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
Water Resources Series No. 84
INSTREAM SALMONID HABITAT EXCLUSION
BY ICE-COVER
Lora S. Johnson Thomas A. Wesche
Donna L. Wichers James A. Gore
May, 1982
Water Resources Research Institute
University of Wyoming
Laramie, Wyoming
Completion Report #2 of 2
Presented to
Office of Water Research and Technology,
Wyoming Game and Fish Department, and
Wyoming State Engineer's Office
on
Project No. B-038-WYO
Agreement No. 14-34-0001-8130
The work upon which this publication is based was supported in part by funds provided by the Office of Water Research and Technology, Project B-038-WYO, U.S. Department of the Interior, Washington, D.C., as authorized by the Water Research and Development Act of 1978.
Contents of this publication do not necessarily reflect the views and policies of the Office of Water Research and Technology, U.S. Department of the Interior, nor does mention of trade names or commercial products constitute their endorsement or recommendation for use by the U.S. government.
ABSTRACT
Research was conducted on a smaller Wyoming foothills stream to attempt to develop a method for predicting the effect of winter ice-cover on the habitat available to a brown trout population. Predictive equations were developed relating percent habitat excluded to the following parameters: days from the winter solstice, degree days of frost, mean water velocity, and mean effective water depth. The resultant method could be of value to resource managers in determining winter instream flows to maintain trout habitat.
Key Words:
Trout habitat, instream flow, winter habitat, ice formation,
ice hydrology, habitat exclusion, brown trout
ACKNOWLEDGEMENTS
The authors wish to express their appreciation to the following agencies for providing the funds necessary to conduct this research: the Office of Water Research and Technology, U.S. Department of the Interior; Wyoming Game and Fish Department; and Wyoming State Engineer's Office.Appreciation is also expressed to the many WRRI and University of Wyoming personnel who assisted in various aspects of the project.
TABLE OF CONTENTS
Page
INTRODUCTION. . . . . . . . . . . . . . . . . . . . . . . . . 1
DESCRIPTION OF STUDY AREA . . . . . . . . . . . . . . . . . . 7
METHODS . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
RESULTS AND DISCUSSION. . . . . . . . . . . . . . . . . . . . 13
SUMMARY AND CONCLUSIONS . . . . . . . . . . . . . . . . . . . 27
REFERENCES. . . . . . . . . . . . . . . . . . . . . . . . . . 28
LIST OF FIGURES
Figure Page
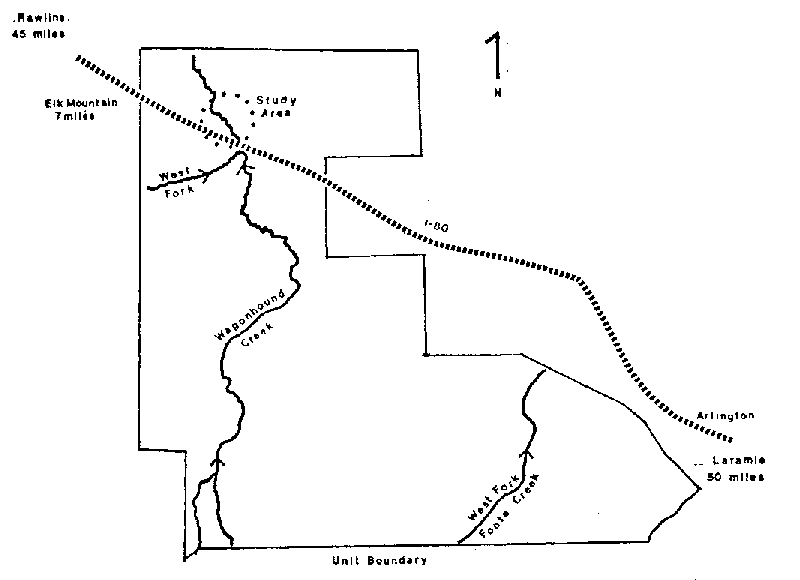
1. Map depicting location of study area within the Wyoming
Game and Fish, Wicks Brothers' Management Unit. . . . . 8
2. Observed and predicted values for percent habitat
excluded for the riffle . . . . . . . . . . . . . . . . 15
3. Observed and predicted values for percent habitat
excluded for the run. . . . . . . . . . . . . . . . . . 16
4. Observed and predicted values for percent habitat
excluded for the pool . . . . . . . . . . . . . . . . . 17
LIST OF TABLES
Table Page
1. Values of variables used for the multiple linear
regression. . . . . . . . . . . . . . . . . . . . . . . 14
2. Analysis of variance for the predictive equations
describing percent habitat excluded . . . . . . . . . . 18
3. Empirically derived "a" values . . . . . . . . . . . . . 22
4. Values of variables used in example of proposed
model applications. . . . . . . . . . . . . . . . . . . 25
INTRODUCTION
In recent years, much research has centered around the determination of instream flows necessary to maintain salmonid habitat in light of increasing out-of-channel water demands. A review of existing instream flow methodologies for fisheries (Stalnaker and Arnette, 1976; Wesche and Rechard, 1980) indicates that while a great deal is known about habitat requirements during the ice-free period of the year and subsequent methods for measurement of this habitat, little research effort has been extended regarding habitat conditions and requirements during the critical winter season, when complete ice-cover blankets many of our northern latitude streams. It is hoped that this report will help to fill this knowledge gap.The need for winter studies on freshwater fish populations was recognized as early as 1935 by Hubbs and Trautman. At that time the interest was centered around over-winter survival of stocked fish. Today's interests in winter data also center around survival of wintering fish, but as related to determination of instream flows to maintain these fisheries during winter low-water conditions. Unfortunately, little research has been done on fish winter movements, feeding needs and habits, cover needs, microhabitat occupation, or other aspects of life-history under ice-cover. A search of the literature indicates that no one has ever determined any salmonid habitat or instream flow requirements for streams with complete ice cover. For this there is a very definite need.
Maciolek and Needham (1952) conducted winter studies on Convict Creek, California (elevation 7,200 ft) to determine the effects of winter conditions on trout and trout foods. Extensive ice formations and freezing water temperatures were present, but none of the four controlled experimental sections were ever completely frozen over. Brown and rainbow trout were found to be active and feeding even at water temperatures of 32°F, contradicting the popular belief that trout are less active in winter. Some trout were caught by angling with bait when water temperatures ranged from 35°F to 42°F. When available, surface sheet ice was observed to be used as cover by trout. Maciolek and Needham also observed that Convict Creek supported higher standing crops of benthic organisms during the winter than in summer. This was attributed to the fact that the bulk of organisms are present in immature stages, unable to emerge until warmer weather. Stomach content analysis of trout showed that 50 percent of the total food ingested is digested in 14 hours at temperatures between 32°F and 35°F.
A study of the over-winter survival of summer-planted hatchery- reared trout (catchable size) and wild trout was also conducted at Convict Creek, California, by Reimers (1963). He found that general body condition of the summer-planted hatchery trout declined continuously from time of planting throughout the winter season. With the advent of spring and warmer water temperatures, high mortality rates of the hatchery trout occurred due to increased activity of trout in a weakened condition. Wild trout, however, were able to survive the onset of warmer temperatures and increased activity due to adequate energy reserves. Reimers noted that fluctuating periods of freezing temperatures (32°F) with warmer temperatures (40°F) caused weakened conditions during warmer periods. He also noted that a stable freezing water temperature is a successful mechanism for survival of over-wintering trout due to the reduction of metabolism to near-basal levels and the subsequent reduction in use of fat reserves. Winter intake of food by wild trout was often less than half that normally consumed in the summer and fall. Reimers stated that winter food availability should be based upon the extent of feeding rather than benthic samples as these samples may falsely indicate what food is actually available.
An underwater observation tank was used by Needham and Jones (1959) In Sagehen Creek, California (elevation 6,337 ft) to observe trout behavior during the winter season. Air and water temperatures, solar radiation, water levels, and general fish activity were moni- tored from the station. Consistent with the findings of Macloiek and Needham (1952), Needham and Jones observed trout actively feeding when water temperatures were between 32.0°F and 33.0°F. Trout actively swam up to drifting food particles, selectively ate them, and also fed directly off the bottom of the stream. Bottom macrofauna was abundant and active. Anchor ice, when dispersing and breaking up, was noticed to dislodge considerable numbers of invertebrates, thus making food available to trout. Brown, Clothier, and Alvord (1953) could not detect any change in numbers of bottom organisms where anchor ice formed, but did state that bottom organisms could be dislodged and carried away with ice dispersal.
Needham and Jones noticed that during winter, trout preferred areas of very dark cover. Ice and snow banks were used as cover, and a definite territorial behavior was exhibited for sheltered locations. Other conclusions by the authors were: (1) high winter mortalities of trout were probably not the result of low temperatures or lack of food, but due to physical catastrophes such as floods, entrapment under collapsed snow banks, or stream dewatering; and (2) 32°F is within the zone of tolerance of trout; and (3) trout can resist water temperatures below 32°F for short periods of time.
Benson (1955) studied anchor ice in the Pigeon River, Michigan, in attempts to determine the possible influence of ice on trout stream ecology. Anchor ice was not found to affect trout eggs as they were buried in gravel below the influence of anchor ice. Trout fry in the egg sac stage, however, were found to be highly vulnerable to mortality if they were emerging at the time of anchor ice formation. Contrary to the findings of Maciolek and Needham (1952) and Needham and Jones (1959), trout in the Pigeon River did not actively feed, and their coefficient of condition was low. All trout were found in quiet eddies and under the stream banks. Benson questioned whether trout actually benefited from winter feeding, and doubted the value of making food available for trout during the winter.
The effects of ice, temperature, and fluctuating water levels on benthic fauna and movements of trout were investigated by Logan (1963) in Bridger Creek, Montana. Severe winters with prolonged periods of below-freezing air temperatures were characteristic of the study site, but as with all the previous studies, surface ice never entirely covered the stream. Portions of surface ice that were occasionally present were found to have no effect on the abundance of bottom organisms. Again, numbers of organisms were high during the winter months. However, abundance of drift organisms were high during the winter months. However, abundance of drift organisms was low during the late fall and winter due to low streamflows. Conclusions Logan made pertaining to winter movements of trout in Bridger Creek were: (1) more than 50 percent of trout within the section migrated no farther than 150 feet from their original location of capture; (2) movements appeared to be slightly greater In December, January and February, when temperatures were low and surface ice was present; and (3) seasonal location preferences occurred-trout moved out of spring, summer and fall inhabited pools to shallower water under surface ice cover in winter.
Chapman (1966) discussed the aspects of food and space as regulators of salmonid populations in streams. In areas where food is more available. Chapman reasoned that territory size of fish is reduced because less space is required to obtain food. In this case, population densities may be greater in a smaller area, with less territorlality. Chapman also proposed that in spring, summer, and fall, density is regulated primarily by the space-food convention while, in winter, density may be regulated by space alone, as related to protection.
In 1968, Chapman and Bjornn reviewed the distribution of salmonids in streams as related to food and feeding. Conclusions of the authors were: (1) during the period from spring to fall most salmonids occupied stream depths and water velocities proportionate to their body size, moving to faster, deeper areas which provide greater food supply and cover as they grow larger; (2) winter cover was important in holding over-wintering fish, especially substrate areas with large rocks. Fish moved closer to the substrate as water temperatures approached freezing; (3) hiding behavior was common during winter among stream salmonids, and was often preceded by down- stream movements in the fall.
Although the findings of these authors relate to possible winter effects on trout, none actually defined the specific microhabitat needed by trout in terms of such physical parameters as water depth, velocity, substrate or cover. Nor does the literature provide insight into the physical exclusion of potential habitat by displacement of the water column by surface ice. The specific objective of this report will be to present equations, based upon field research on a smaller brown trout stream, which relate habitat exclusion through ice formation to such parameters as air temperature, discharge (and correlated mean velocities and water depths), and day length. A report closely related to this one, by Wichers, Johnson, Wesche and Gore (1982), compares two techniques for locating and sampling brown trout microhabitat under complete ice cover.
DESCRIPTION OF STUDY AREA
The study area was located in Carbon County, Wyoming, on Wagon- hound Creek where it flows through the north portion of the Medicine Bow Big Game Winter Range, managed by the Wyoming Game and Fish Department. This property is also referred to as the Wicks Brother's Ranch. The study section was located in the southwestern quarter of Section 5, T. 19 N., R. 79 W., and was bounded on the south, at its upstream end, by Interstate 80 (see Figure 1).Wagonhound Creek in the area of the study section is an ungaged, meandering foothills stream at an elevation of 7,420 ft (2,261 m). The stream is characterized by a typical riffle-pool-run complex with stream widths varying from 15-45 ft (4.5-14 m).
Mean water velocity through the 2,000 ft (610 m) study section was measured by a dye dilution study at 0.254 ft/s (7.74 cm/s) in September. Discharge from September through March ranged from 2.59 to 7.70 cfs (.073 to .216 m3/s). Total alkalinity averaged 339 mg/l and pH was recorded at 8.2 for September and October. Water temperature, as measured by a mercury thermometer and recording thermograph to the closest degree Centigrade, was consistently 0°C after ice cover came on at the end of November.
The general topography of the area is rolling foothills covered with sagebrush (Artemesia sp.) and mountain mahogany (Cercocarpus montanus). Summer riparian land use immediately upstream of the study area is cultivated hay fields. During winter months, land use reverts to an elk wintering area. Summer cattle grazing is the primary land use directly adjacent to the study section. Riparian vegetation includes willow (Salix sp.), rose (Rosacea sp.), and cottonwood (Populus sargentell).
METHODS
Measurements of ice depth for the riffle, run and pool areas were made along transects at each site. When possible, these measurements were made twice weekly from January 15, 1980 to March 25, 1980. Holes in the ice were spaced 3 ft (0.91 m) apart in the run and pool areas. Spacing was 1.5 ft (0.46 m) in the riffle in order to compute discharge. Total water depth and ice depth were recorded at each hole and velocity measurements were taken at the riffle area to compute discharge (Buchanan and Somers, 1969). Minimum and maximum air tem- perature data were obtained from the National Oceanic and Atmospheric Administration (NOAA) station at Elk Mountain, Wyoming.From the transect data taken at the riffle, run, and pool areas, the percent habitat excluded was calculated as the cross-sectional area of ice divided by the potential cross-sectional area of water if ice cover had not been present (this area was based on water depths welled up in each hole through which measurements were taken). Degree days of frost, S, were then computed from the day sheet ice first appeared, to, in the following way:
t
S = ò (32-Ta) dt (1)
to
where Ta is the mean daily temperature of the air in degrees
Fahrenheit (Michel, 1971). This was modified to
t
S = å (32 - Ta)
to
in order to compute S using mean dally temperature. Each day in the
sampling period for which ice measurements were made was numbered
successively. This numbering was to serve as an index of solar radia-
tion. As the period for which ice measurements were taken was
following the winter solstice, all numbering was increasing. This was
to reflect increasing day length and a general trend in increasing
intensity of solar radiation as the altitude of the sun increased. If
sampling had occurred prior to the winter solstice, the rationale
behind the numbering would have dictated a decrease in the numbering
to reflect shortening days.
The effective cross-sectional area of water was calculated from the transect data for each site by subtracting the cross-sectional area of ice from the potential cross-sectional area of water. Mean velocities were then calculated by dividing discharge by the effective area of water. Likewise, mean effective depth of water was calculated by dividing the effective area of water by transect length.
Ice formation has been viewed as a process generally controlled by heat balance (Barnes, 1906, 1928; Ashton, 1979; Michel, 1971). Correlation of such instream values as water depth and velocity to ice formation required some experimentation. During the analysis a number of different combinations of variables were used. Ultimately a multiple regression using percent of habitat excluded as the independent variable and day number, degree days of frost, mean effective water depth, and mean velocity as the dependent variables was performed. Exclusion here implies that cross-sectional area of water displaced by ice. This analysis was performed using the statistical computer package, Minitab (Ryan, Joiner, and Ryan, 1978).
RESULTS AND DISCUSSION
Table 1 gives the values of the variables used in the multiple linear regression analyses of ice cover. This regression yielded the following predictive equations:
Riffle: % Excluded = 138 + .326 (Day No.) - .0263 (S) -
200 (Mean Effective Water Depth) -
11.7 (Mean Velocity) (2)
Run: % Excluded = 104.0 - .655 (Day No.) + .0359 (S) -
82.6 (Mean Effective Water Depth) -
66.4 (Mean Velocity) (3)
Pool: % Excluded = 8.53 - 1.31 (Day No.) + .0974 (S) +
50.4 (Mean Effective Water Depth) -
.934 (Mean Velocity) (4)
Observed and predicted values are shown in Figures 2, 3, and 4.
Analysis of variance tables for the regression equations are given in
Table 2.
The following discussion has been drawn from a summary of the current state of knowledge on ice formation published by the Cold Regions Science and Engineering Laboratory entitled Winter Regime of Rivers and Lakes, by Bernard Michel (1971). The process by which ice cover forms on smaller streams and brooks (such as Wagonhound) is known as shore ice formation. In larger rivers "frazil evolution" is the significant process in the formation of ice cover. Shore ice is
TABLE 1
VALUES OF VARIABLES USED FOR THE MULTIPLE LINEAR REGRESSION
________________________________________________________________________________________________________________________________
Riffle (r2 = .95) Run (r2 = .89) Pool (r2 = .83)
Mean Mean Mean
Effective Mean Water Effective Mean Water Effective Mean Water
Water Depth Velocity % Habitat Water Depth Velocity % Habitat Water Depth Velocity % Habitat
Day No. S (ft) (ft/s) Excluded (ft) (ft/s) Excluded (ft) (ft/s) Excluded
1 324.5 0.2625 0.57 71 0.3846 0.39 65 0.6000 0.12 69
8 382.0 0.483 0.76 42 0.5467 0.57 27 0.6142 0.29 66
10 400.5 0.4325 0.43 37 0.4625 0.41 38 0.5780 0.15 62
29 683.0 0.4367 0.60 29 0.5375 0.49 34 0.5577 0.23 65
31 696.5 0.4862 0.48 30 0.6250 0.38 29 0.5173 0.23 67
36 736.0 0.5004 0.49 26 0.5529 0.44 27 0.5906 0.21 62
38 727.0 0.5692 0.54 11 0.7408 0.41 21 0.6454 0.24 59
43 743.0 0.5283 0.43 25 0.5529 0.41 31 0.6502 0.17 57
50 737.5 0.6248 0.41 3 0.7312 0.39 11 0.6889 0.18 51
57 771.0 * * * 0.6662 0.48 11 1.019 0.16 58
63 728.5 * * * 0.6187 0.47 8 1.092 0.13 57
68 796.5 * * * 0.6875 0.40 0 0.8919 0.15 59
________________________________________________________________________________________________________________________________
*No data due to growth of snow pack (depths in excess of 10 ft).
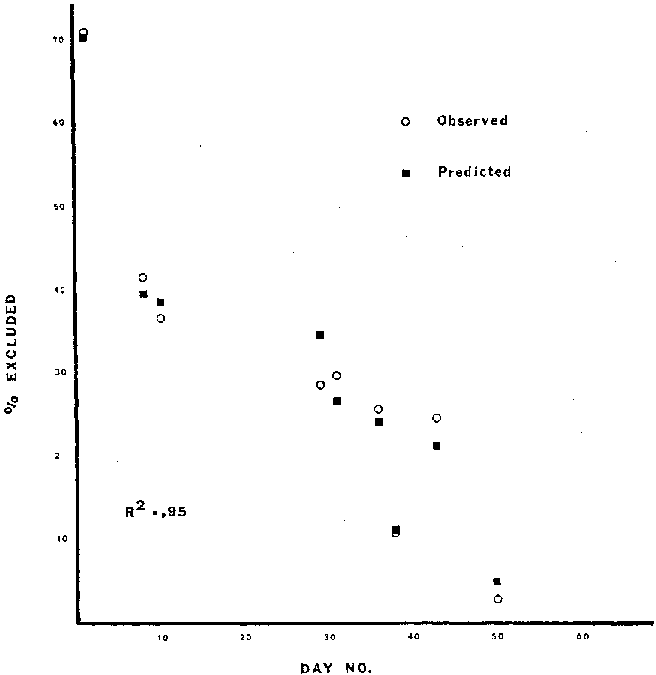
Figure 2. Observed and predicted values for percent habitat
excluded for the riffle
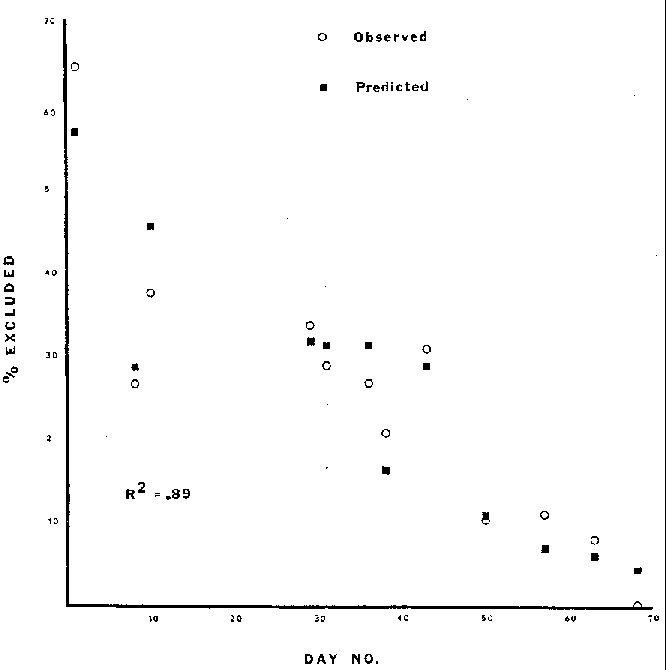
Figure 3. Observed and predicted values for percent habitat
excluded for the run
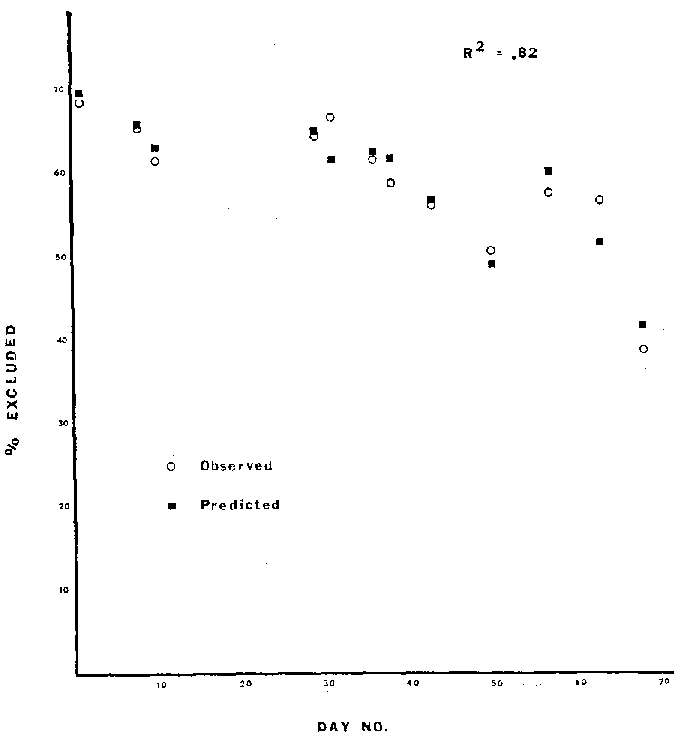
Figure 4. Observed and predicted values for percent habitat
excluded for the pool
TABLE 2
ANALYSIS OF VARIANCE FOR THE PREDICTIVE EQUATIONS DESCRIBING
PERCENT HABITAT EXCLUDED
________________________________________________________________________________________________________
Degrees of Sum of Mean
Freedom Squares Squares F-Value F (.05) Comments
RIFFLE
Due to:
Regression 4 2931.3 732.8 40.26 6.39 Regression
correlation
is significant
Residual 4 72.9 18.2
Total 8 3004.2
Run
Due to:
Regression 4 3006.4 751.6 23.3 4.12 Regression
correlation
is significant
Residual 7 225.3 32.2
Total 11 3231.7
POOL
Due to:
Regression 4 657.9 164.5 14.3 4.12 Regression
correlation
is significant
Residual 7 80.7 11.5
Total 11 738.7
________________________________________________________________________________________________________
the growth of ice proceeding from the shore out into the stream as ice
is nucleated at the banks, which are more conductive and thus cooler.
Ice can also progress from emerging boulders and submerged objects
where anchor ice has formed, anchor ice being the accumulation and
growth of frazil particles on objects such as rocks and weeds. Frazil
is defined here as a group of individual ice crystals having the form
of small discoids or spicules which are formed in supercooled
turbulent water (Michel, 1971).
The initial lateral formation of the shore ice described above
can be represented by the heat transfer equation:
Yc = Cw Vw D Tw (5)
where Cw is a constant, Vw and Tw are the water velocity and tempera-
ture difference above freezing (Michel, 1971). Empirical data suggest
that an ice cover may grow by this process at any water velocity if
the temperature of the water is close enough to the freezing point.
Once surface ice is formed vertical growth of transparent black
ice in the presence of snow (where the surface of the snow is the
temperature of the air) is described by the heat transfer equation:
Ki (32 - Ta) dt = Ks (Ts - Ta) dt = giLdh (6)
________ _______
h h
where: Ta = temperature of the air, °F
Ts = temperature of snow ice interface, °F
gi = specific weight of ice
Ki = coefficient of thermal conductivity of ice
Ks = coefficient of thermal conductivity of snow
L = latent head of fusion of ice
h = thickness of ice sheet at time t
h s= depth of snow
This equation can be integrated between limits of ho to h for
a constant snow thickness hs, which gives.
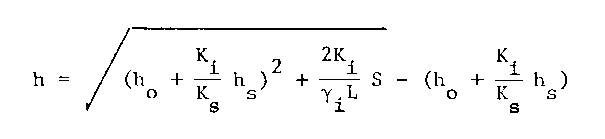 (7)
(7)
In the absence of snow, black ice growth can be represented by:
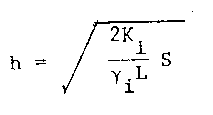 (8)
(8)
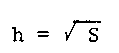 (9)
(9)
For making predictions of ice thickness, it is not possible to correctly estimate whether ice growth will be in the presence of snow, by black ice formation, or by snow ice formation. Therefore, the formula used for engineering purposes is:
Z = a (S)0.5 (10)
where: Z = thickness of the total solid part of ice in inches
S = degree days of frost
a = coefficient derived from experience to correct for
meteorological conditions
Values of "a" for a small river range from 0.2-0.4 (Michel,
1971). This description would presumably fit the riffle-run area. A
windy lake with no snow has a value of 0.8. This description might
more accurately reflect a pool situation. In determining "a" values
for the riffle, run and pool areas of Wagonhound, this formula came
close to predicting the thickest ice cover encountered where "a"
values for the riffle, run and pool were 0.47, 0.51, and 0.93,
respectively (see Table 3).
It seems intuitively reasonable that at a given temperature a stream with low flows would have a thicker ice cover and vice versa. The equation, Z = a (S)0.5, does not predict such differences or differences in ice thickness for different types of areas within the stream (i.e., riffle, run, pool). Using heat balance equations to predict ice thickness also does not allow for management of flows to keep areas open to increase survival.
At Wagonhound the stream is totally ice-covered for a period of approximately three months. The major objective of studying the ice cover was to determine how much of the stream was physically excluded due to ice and develop a predictive model. Thus, by managing winter flows a predictable amount of "habitat" would be left ice-free, where it is assumed that all free water would be available as potential habitat.
TABLE 3
EMPIRICALLY DERIVED "a" VALUES
___________________________________________________________________________________________________
Riffle Run Pool
S Z (inches) a Z (inches) a Z (inches) a
324.5 8.52 0.4729 9.12 0.5063 16.8 0.9326
382.0 3.60 0.1842 2.76 0.1412 12.48 0.6385
400.5 3.24 0.1619 3.72 0.1859 12.48 0.6416
683.0 4.20 0.1607 3.48 0.1331 12.96 0.4959
696.5 2.52 0.0955 3.24 0.1228 13.32 0.5047
736.0 2.16 0.0796 4.20 0.1548 12.24 0.4511
727.0 0.84 0.0311 2.64 0.0979 11.64 0.4317
743.0 2.28 0.0836 3.24 0.1189 10.92 0.4006
737.5 0.24 0.0088 1.08 0.0398 9.24 0.3402
771.0 - 1.20 0.0432 17.28 0.6223
728.5 - 0.72 0.0267 16.92 0.6269
796.5 - 0.72 0.0255 7.44 0.2636
___________________________________________________________________________________________________
An attempt to relate velocity to ice thickness on the Tongue
River met with only moderate success (Bovee, Gore and Silverman, 1978)
(non-linear correlation coefficients of -.462 to -.532). When this
correlation was attempted on Wagonhound, not even a moderate correla-
tion could be found (r2 = .05). This disparity may be explained by
the differences that exist between conditions at the Tongue and at
Wagonhound. Due to the size of the Tongue, theoretically, ice forma-
tion is mostly by frazil evolution. At Wagonhound, ice formation is
primarily by shore ice. Also, the snow cover on the lower Tongue is
insignificant (snow is generally blown off the river) (Bovee et al.,
1978), while at Wagonhound snow cover is extensive (drifts of 4 to 8
ft covering the stream). For Wagonhound good results for relating
flow dependent variables to ice cover were obtained through a multiple
regression of time, S, effective depth of water and mean water
velocity against percent of habitat excluded.
To illustrate the application of this correlation to a management situation, Wagonhound can be used as an example. From the standpoint of food production, the riffle and run areas are the most important, based upon the results of sampling done in conjunction with this study. To maintain the brown trout in winter, it appears that areas of slow velocity, but fairly deep water are preferred habitat as in a pool. Thus, by selecting either a preferred velocity or a preferred depth and varying discharge in a stream with known widths for riffle- pool-run areas, mean effective depth or mean velocity can be obtained. Then by selecting a date which would correspond to a certain number of days prior to or after the winter solstice and a corresponding S (calculated from temperature records), a predictable amount of habitat should be available.
One extreme which can be considered is the situation where 100 percent of the riffle area would be excluded. This would effectively destroy the benthos (Brown, Clothier and Alvord, 1953). The other extreme is that of 0 percent habitat excluded; however, due to the large influence of temperature on the formation of ice, no matter what the discharge, this situation would be highly unlikely.
If the goal is to maintain 50 percent of the riffle open (for benthos) and a velocity of 0.50 fps (for the brown trout) and day 1 is selected where S = 324.5, then effective depth in the riffle can be determined using the predictive equation for the riffle which, in this case would be:
.50 = 138 + .326(1) - .0263(324.5) - 200(D) - 11.7(.50) (11)and effective depth would be 0.37 ft. Recommended discharge would then be:
Q = Mean Depth x Width x Mean Velocity (12)
where W is 24 ft and depth and velocity have been determined, so
Q = 4.44 cfs. Table 4 gives the associated values in the riffle, run
and pool for this example.
It would be necessary to verify the predictive equations developed for Wagonhound on other streams where ice cover forms primarily by shore ice and snow cover is present before applying them
TABLE 4
VALUES OF VARIABLES USED IN EXAMPLE OF PROPOSED MODEL APPLICATIONS
_________________________________________________________________________________________________________
Riffle Run Pool Comments
Day Number 1 1 1 Arbitrarily selected.
S 324.5 342.5 342.5 Value associated with day 1.
% Habitat Excluded 49.94 52.74 63.34 Riffle: Value set as management goal;
yields a given discharge.
Run and Pool: Values arising form
recommended discharge for riffle
which allows for use of the predic-
tive equations for the run and pool.
Mean Effective .37 .40 .49 Riffle: Value obtained through predic-
Water Depth (ft) tive equation when V=.5, day no.=1,
S=324.5, and % habitat excluded=50%.
Run and Pool: Values obtained through
use of Q=WxDxV, where Q=4.44, W=48,
V=.46 for run and .19 for pool.
Mean Water Velocity .50 .46 .19 Riffle: Value set as management goal.
(cfs) Run and Pool: Empirically observed
values when riffle velocity is .5
cfs.
Width of Channel (ft) 24 24 48 Field measurements
Discharge 4.44 4.44 4.44 Discharge originally calculated from
riffle data where V=.5, W=24, and
D=.37.
_________________________________________________________________________________________________________
to a management situation. Development of predictive equations for
streams not experiencing the same conditions as Wagonhound would
optimize the technique as a management tool.
SUMMARY AND CONCLUSIONS
The predictive equations relating day, S, mean water velocity, and mean depth to percent habitat excluded are:RIFFLE: % = 138 + .326(Day) - .0263(S) - 200(D) - 11.7(V) RUN: % = 104.0 - .655(Day) + .0359(S) - 82.6(D) - 66.4(V) POOL: % = 8.53 - 1.31(Day) + .0974(S) + 50.4(D) - .934(V)These predictions accurately reflected the conditions on Wagonhound; however, to apply them elsewhere would require verification at another stream of the same order and experiencing similar weather conditions.
While winter instream flow requirements are nebulous, stream managers can at the minimum make habitat available on regulated streams by estimating what areas are the most critical and how much habitat needs to be made available. Knowledge of habitat preferenda at other seasons of the year and the relative size of the stream under consideration would aid in making the subjective judgment of how much habitat is necessary. A given discharge should then satisfy these conditions as predicted by the above equations.
REFERENCES
Ashton, George D. 1979. River ice. American Scientist, 67(1) :38-45.Barnes, H. T. 1906. Ice Formation. John Wiley and Sons, New York.
Barnes, H. T. 1928. Ice Engineering. Renouf Publishing Company, Montreal.
Benson, Norman. 1955. Observations on anchor ice in a Michigan trout stream. Ecology, 36(1) :529-530.
Bovee, K. D., J. A. Gore, and A. J. Silverman. 1978. Field testing and adaptation of a methodology to measure "in-stream" values in the Tongue River, Northern Great Plains (NGP) Region. U.S. Environmental Protection Agency, EPA-908/4-78-004A.
Brown, C. J. D., W. D. Clothier, and W. Alvord. 1953. Observations on ice conditions and bottom organisms in the West Gallatin River, Montana. Proceedings of the Montana Academy of Sciences, 13:21-27.
Buchanan, Thomas J., and William P. Somers. 1969. Discharge measure- ments at gaging stations. Techniques of Water-Resources Investigations of the U.S. Geological Survey, Book 3, Chapter A8, U.S. Government Printing Office, Washington, B.C.
Chapman, D. W. 1966. Food and space as regulators of salmonid populations In streams. Am. Natur., 100:345-357.
Chapman, D. W., and T. C. Bjorn. 1968. Distribution of salmonids in streams with special reference to food and feeding. In Symposium on Salmon and Trout in Streams, H. R. MacMillan Lectures in Fisheries, Univ. of British Columbia, Vancouver, B.C., pp. 153-176.
Hubbs, C. L., and M. B. Trautman. 1935. The need for Investigating fish conditions in winter. Trans. Am. Fish. Soc., 65:51-56.
Logan, S. L. 1963. Winter observations on bottom organisms and trout in Bridger Creek, Montana. Trans. Amer. Fish. Soc., 92:140-145.
Maciolek, John A., and P. R. Needham. 1952. Ecological effects of winter conditions on trout and trout foods in Convict Creek, California. Trans. Amer. Fish. Soc., 81:202-217.
Michel, Bernard. 1971. Winter regime of rivers and lakes. Cold Regions Research and Engineering Laboratory. Monograph III-Bla. Hanover, New Hampshire.
Needham, Paul R., and Albert C. Jones. 1959. Flow, temperature, solar radiation, and ice in relation to activities of fishes in Sagehen Creek, California. Ecology, 40:465-474.
Reimers, Norman. 1963. Body condition, water temperature, and over-winter survival of hatchery-reared trout in Convict Creek, California. Trans. Am. Fish. Soc., 92(1) :39-46.
Ryan, Thomas A., Jr., Brian L. Joiner, and Barbara 1. Ryan. 1978. Minitab II - Reference Manual. Duxbury Press, North Scituate, Massachusetts.
Stalnaker, C. B., and J. L. Arnette. 1976. Methodologies for the determination of stream resource flow requirements: An assessment. Report prepared for U.S. Fish and Wildlife Service, Office of Biological Services, by Utah State University, Logan. 199 p.
Wesche, T. A., and P. A. Rechard. 1980. A summary of instream flow methods for fisheries and related research needs. Elsenhower Consortium Bulletin #9. 122 p.
Wichers, D. L., L. S. Johnson, T. A. Wesche, and J. A. Gore. 1982. Two techniques for locating and sampling brown trout microhabitat under complete ice cover. Water Resource Series Publication No. 83, Wyoming Water Resources Research Institute, University of Wyoming, Laramie (in press).
Water Resources Series List
Water Resources Data System Library |
Water Resources Data System Homepage