WRDS Library [Home]
Digital Library Publications Videos Card Catalog

Chapter II
Literature Review

Agricultural productivity in many arid and semi-arid areas of the world depends largely on irrigation. In 1979 it was estimated that only 13 percent of the total arable land in the world was irrigated. However, the value of the crops produced on the irrigated land was 34 percent of the total value of the world's agricultural crops (Jensen, 1983). Surface irrigation (gravity flow of water over the ground surface) is the oldest irrigation method, and it is still the most common irrigation method used throughout the world. Hillel (1989) gives an estimate that more than 95 percent of the world's irrigated land is irrigated using surface irrigation.

The effects of irrigation can be both beneficial and harmful, and the amount of harm or benefit to the land depends on the proper management and use of available water resources. Barren deserts can be made productive farms with the addition of proper amounts of irrigation water. In semi-arid areas where reliable irrigation water can complement water received from intermittent rains, crop yields can be increased significantly over what is produced with dryland farming. However, the excessive application of water without proper drainage has brought salinization, waterlogging, and a total loss of productivity to some agricultural areas. Other environmental problems also occur if the irrigation water is not carefully and efficiently used. Too much irrigation water applied to fields often results in the leaching of pesticides and fertilizers from the crop root zone down into the ground water causing possible health hazards to people who use water from nearby wells. Excess irrigation water that does not infiltrate the soil often carries chemicals and large amounts of sediment with it as it runs off of the field. As the field runoff returns to streams or rivers, it can cause water quality problems for downstream wildlife and water users (Bowman, 1971).

Water use conflicts have arisen in many irrigated areas where good quality water is in short supply. Competition for water use between agriculture and municipalities has led to an increase in the cost of irrigation water in some areas. Increased water costs, higher quality discharge requirements for agricultural runoff, and problems with groundwater pollution have prompted many farmers and irrigation districts to make improvements which will enhance water use efficiency (Jensen, 1983).

WATER MEASUREMENT
Water measurement is essential to the effective use of irrigation water. Examples of the importance of irrigation flow measurement are discussed in the following pages.

Walker (1972) describes some problems of irrigation districts in the Sevier River Basin in Utah. By 1890 all the land along the river that could be developed by direct diversion had been brought under cultivation. By 1922 enough reservoir capacity had been developed to completely control the flow of the river in all subsequent years except for two. The area is semi-arid to arid and years of drought are common.

In spite of complete river control and many years of drought, the average on-farm water use efficiency was below 45 percent. Rather than being stored for dry years, extra water in wet years is lost due to poor efficiencies and excess diversions. Canal conveyance efficiency was poor until canal lining was installed, but this still left room for improvement in canal management and on-farm water management. Good flow measurement is essential in improving the performance of the system.

Some of the problems found in the Sevier River Basin may be typical of many old canal systems in the western U.S. Most canal systems were built when water seemed cheap and abundant, and flow measurement structures were not initially installed as a part of these systems.

In the early years of the system on the Sevier River, an engineer was hired to design and install gates which could measure the flows delivered to the farmers from the system. The gates, called Cotteral gates after the engineer who designed them, were calibrated and installed, and the discharge curves for the gates were used as a basis of charging the farmers for the water delivered by the canal company. By 1960 almost all of the Cotteral gates had been replaced by different turnout gates. More recently some canal lining has been completed, and with the lining came replacement of all the outlet gates. The canal company discovered that their estimated delivery losses actually increased from 25 to 35 percent after having made the improvements to the canal! The canal lining had reduced seepage losses, but the higher velocities in the channels and the newer gates resulted in farmers getting more water than was being saved by the canal lining. The canal company was still using the Cotteral discharge curves to determine water delivered to the farmers even though there weren't any Cotteral gates in the system. There were a number of different types of outlet gates used in the system, but when the Cotteral gates had been replaced, the new gate discharge rating curves were not developed and used. Only by updating the discharge rating curves for the various gates currently in use could the canal companies get a more reasonable estimate of water deliveries and losses.

Other problems were found with the system management. One canal company had four "water masters" in five years. With each new water master came a period of high losses and low efficiency until enough experience was gained to properly manage the system. "The entire system was an experience rated system of turns, notches, pegs, holes, and threads" (Walker, 1972). However, once enough experience was gained to master the system, the system losses decreased by as much as 20 percent. This type of experience based water control system is common with older canals.

Walker (1972) estimated that using a combination of surface and underground waters (pump from the aquifers in dry years), limiting diversions in wet years, and improving efficiency by 10 percent would eliminate water shortages on the farms currently under irrigation. He also noted that adopting standard structures and methods, together with measurement controls at key points in the system, should provide a base for continuous system improvement. The farmers need to know what the flow is to their fields so they can keep track of their allotment of water and use it most effectively. Standard measurement and outlet structures could allow all farmers on the system to be charged by the same standards and allow the farmers to know what their flowrates are simply by being familiar with the discharge characteristics of the outlets. Experience indicates that farmers are not inclined to use devices which require numerous measurements and complicated mathematical formulas or volumes of discharge tables; they prefer structures gauged for reading the discharge directly and flow measurement devices which are as inexpensive and simple as possible (Walker, 1977).

Good water measurement is essential even where water shortages do not exist; the lack of good water measurement can cause drainage problems, excessive seepage losses, canal breaks, poor on-farm water practices, excessive erosion and sedimentation, and poor water quality. This is demonstrated by two older water districts in Idaho; one is a large district of 65,000 acres, and the other is only 990 acres. No flow measurement structures were used in the distribution systems of either district. After many years of operation with excess water deliveries, many farms in the 65,000 acre district show reduced productivity due to problems caused by a rising water table. The crop production of farms in this district is only about 80 percent of the production of farms in a neighboring district with similar soil and climate conditions, and the neighboring district only uses about one quarter as much water (Schaack, 1975). The canal in the 990 acre district carries about 55 cfs and is composed entirely of earthen channels with wood and concrete structures used for control. The farms all use surface irrigation to apply the water. The overall irrigation efficiency is less than 20 percent, and the area is plagued by high water tables (Busch, 1975). In these districts, excess water caused decreased productivity. Water measurement is essential to good water management for both limited and abundant supplies of water.

SHARP CRESTED WEIRS
Sharp crested weirs are relatively simple devices for open channel flow measurement. There are many types of sharp crested weirs in use, but the most common are rectangular weirs, suppressed rectangular weirs, triangular (V-notch) weirs, and trapezoidal (Cipolletti) weirs (Figure 1). All of these weirs have a number of features in common: the weir crest is a sharp metal plate, the flow jet over the crest must be fully aerated, and the discharge is proportional to the upstream head on the weir.

Many discharge equations for different types of weirs have been developed in laboratory experiments. Schoder (1929) published the results of over 2,000 discharge measurements for 1,512 different heads on rectangular suppressed weirs of different heights and with different velocity profiles. These experiments were performed at Cornell University between 1904 and 1920 and utilized an open channel with a number of weir arrangements. Although weirs of various crest heights were tested, all of the weirs extended the full width of the channel (rectangular suppressed weirs). Velocities were measured in the upstream channel, and baffles and stilling rafts were used to produce different velocity profiles. Discharge volumes were measured in a weighing tank at the end of the open channel and weir apparatus.


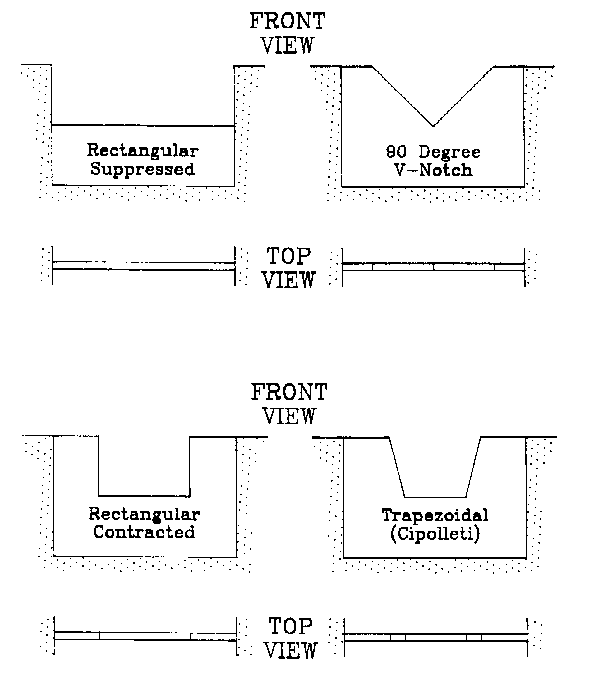
Figure 1. Views of Several Standard Sharp Crested Weirs.

The experimenters arrived at a number of conclusions based on the weir measurements. The Francis formula was found acceptably accurate for weirs with sharp, square edges, a smooth vertical upstream face, a deep upstream pool behind the weir, and negligible effects of approach velocity. It is widely understood that weir discharge equations are accurate to within about two percent as long as the head on the weir is carefully measured; caution should be used when assuming this range of accuracy. The head may be measured carefully, but there are a number of other conditions which may affect discharge by several percent. Slight roundness of the upstream weir edge results in the weir discharge increasing by several percent. Roughness of the weir plate near the crest was also found to increase the discharge even when the crest was sharp. Velocity distribution was also found to influence the weir discharge. It was concluded that if standard weir discharge equations are to be used, careful consideration should be given to measurement of the head on the weir but also to velocities in the upstream channel, weir sharpness, and general conditions of the weir plate (Schoder, 1929).

Ackers (1978) gives five discharge equations for full- width weirs. Each equation is accepted in various parts of the world and for various applications. Ackers points out that no one equation is entirely right and all others wrong; the equations agree with the experimental data obtained by the various experimenters in the development of their formulas. Different weir equations seem to give better results for different conditions (eg. high heads on low weirs or low heads on high weirs). In all cases, the weirs used for flow measurement should be built to standard conditions, and the upstream channel should be straight and uniform for a distance of at least ten times the channel width so that no irregular flow conditions will be present at the weir.

Some of the standard conditions given for small measurement weirs are described by Kraatz and Mahajan (1975). The weir crest should have a square upstream edge with a top thickness of between 1 and 2 mm. The downstream face of the weir should have a camfer of at least 45 degrees so that the water jet springs clear of the weir. For contracted weirs, the crest height should be greater than twice the depth of the maximum head on the weir, and the sides of the weir opening should be at least a distance of twice the head from the side walls of the channel. Conditions other than these could affect the shape of the nappe (the water jet over the weir) and alter the weir discharge. The head on the weir (h) should meet the following criteria: 6 cm <= h <= 60 cm, and the head on trapezoidal and rectangular weirs should be less than or equal to one third of the crest length. Very low heads should be avoided because the jet will cling to the weir face rather than springing clear. The weir crest must be level and straight. The weir crest must be higher than the downstream water surface so that the weir can discharge freely. Sharp crested weirs are not intended to operate under submerged flow conditions.

The use of sharp crested weirs is limited by several constraints. Because weirs trap sediments very effectively, weirs should be used only where the flow is relatively free of sediments and debris. Weirs used in flows carrying sediment should have gates in the bottom that can be opened to flush the sediments from behind the weir, or other methods for periodic sediment removal should be provided to insure that the sediment does not accumulate excessively behind the weir. A free fall of the nappe is required for sharp crested weirs to operate properly, and this requires some fall in the channel. Sharp crested weirs may not be practical to use in channels with very flat slopes because the backwater curve created behind the weir may extend for miles and require expensive raising of the channel banks to contain the water. The bottom of the channel directly downstream of the weir crest is subjected to high pressures due to the impact of the falling nappe, and channel protection is required in this area (Papoutsi-Psychoudaki, 1988). Due to the extensive channel protection that would be required for weirs with high heads and large flow rates, sharp crested weirs are generally limited to relatively small-scale applications (the Bureau of Reclamation, 1974 gives a maximum flowrate in their sharp crested weir discharge tables of about 100 cfs).

LONG CRESTED WEIRS
Long crested weirs provide more weir crest length by installing the weir at some configuration other than perpendicular to the channel. These configurations may be diagonal weirs, duckbill weirs, or labyrinth weirs. Figure 2 gives a plan view of several types of long crested weirs. The benefits of long crested weirs over standard weirs is that long crested weirs will pass more flow with less head variation on the weir than standard weirs. Because the flow is spread out over more crest length, an increase in flow produces a smaller increase in head than occurs for standard weirs.

Labyrinth weirs are simply long crested weirs consisting of a series of duckbill-type weirs placed side by side across the channel. This type of weir has been used for spillway or overflow structures of large reservoirs. They have the advantage of providing long overflow crest lengths even when site constraints require that the spillway channel width be limited. The Ute Dam on the Canadian River in New Mexico uses a 14-cycle labyrinth weir in its spillway. The total crest length is 3,360 feet in a spillway width of 840 feet. The design discharge is 590,000 cfs for a head of 19 feet on the weir (Bureau of Reclamation, 1987). The Beni Behdel Dam in Algeria has a labyrinth weir crest length of 1200 m in a channel 80 m wide and is designed to pass a flood of 1000 m^3/ sec at a head of only 0.5 m. A standard weir 80 m long with a head of 0. 5 m would only pass a flow of about 95 m^3/ sec (Hay, 1970).


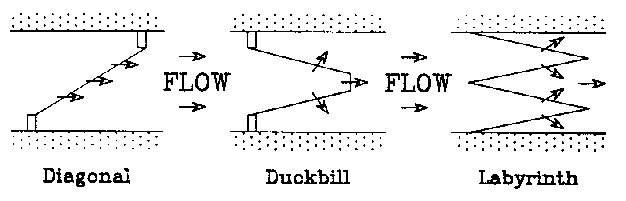
Figure 2. Plan Views of Three Types of Long Crested Weirs.


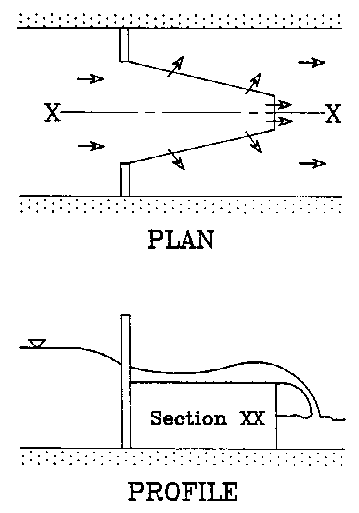
Figure 3. Water Surface Profile of Flow in a Duckbill Weir.

The performance of labyrinth weirs depends on the weir configuration, operating heads, and ratio of weir crest length to channel width. The flow patterns over the labyrinth weir can be very complex. As the flow enters one cycle of the weir, the water surface tends to drop because of the constriction caused by the weir. As the flow continues down the weir, the weir continues to constrict the flow, but the flow rate which approaches the downstream end of the weir is decreasing because of the flow which passes over the weir crest into the downstream channel. The flow passing over the weir crest tends to cause a rise in the water surface in the weir because the water in the weir reacts to the lost flow. The contraction and decreased flowrate create a gradual rise in the water surface as it approaches the downstream end of the weir (a spatially varied flow phenomena). Therefore, the head of the water passing over the weir is not constant for the entire length of the weir crest (Figure 3). This phenomena tends to reduce weir performance at high upstream heads and high approach velocities.

Hay (1970) used labyrinth weir models in a channel 16 ft long 3 ft wide and 1.2 ft deep to test the relationship of weir performance (Ql/Qn) to the following dimensionless parameters: h/p, w/p, l/w, a, and n. Ql is the discharge of the long crested weir, and Qn is the discharge of a normal rectangular weir with the same crest type. The "h" is the head on the weir, and the "p" is the crest height from the bottom of the channel. The width of one cycle of the weir is "w", and "l" is the length of the long crested weir's crest. "a" is the angle of the sides of the weir to the direction of flow, and "n" is the number of cycles of trapezoids or triangles in the long crested weir. The model weir tests showed that performance was independent of n, but it decreased for high l/w and h/p values. Higher a values (triangular plan views) generally showed the best performance as long as there was no nappe interference between neighboring weir cycles. As long as w/p was greater than 2.5, its effect on performance appeared to be negligible.

Duckbill weirs and other long crested structures have been put to use in irrigation projects in Spain and North Africa. Their main purpose is to maintain constant water levels for turnout structures upstream from the weir. This function is very important for providing a fairly uniform discharge through the outlet structures. Canal systems designed to provide water to farmers on demand often have large variations in canal flowrate throughout the irrigation season. Changes in canal flow with water demand causes the flow depths in the canal to vary from day to day and even from hour to hour. When the canal turnout structures are submerged orifice gates, fluctuations in water surface levels in the canal causes discharges to fields through the orifice turnouts to vary. During irrigation, these varying flows reduce the efficiency of field irrigation systems (Clemmens, 1984).

The discharge of long crested weirs for design purposes can be estimated using the following equation:

Q = cBH(3/2)*(2g)^(1/2)

where Q = discharge over the weir (m^3/ sec), c = discharge coefficient, B = crest length (m) , and H = height of water above the weir crest (m). Kraatz and Mahajan (1975) give the following estimates of the discharge coefficients for various types of long creste weirs and for two different crest types: 

                                       Weir Tvpe
        Crest Tvpe          Diagonal   Duckbill Labyrinth
        Unrounded Crest       0.34       0.32      0.31
        Rounded Crest         0.38       0.36      0.34
The authors emphasized that although these coefficients are adequate for use in estimating design flowrates and heads, the coefficients are not calibrated closely enough to use the weirs as accurate flow measurement structures. Although not currently used to measure flow, the long crested weirs have proven to be very effective structures for maintaining relatively constant (within 5 to 10 cm) upstream water surface elevations in spite of variations in the flow in the main canal. These weirs can also pass large flowrates with relatively small changes in head on the weir.

93-13 Table of Contents
Water Resources Publications List
Water Resources Data System Library | Water Resources Data System Homepage