| |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
DESIGN RAINFALL DISTRIBUTIONS
FOR THE
STATE OF WYOMING
Patrick T. Tyrrell
Victor R. Hasfurther August, 1983
Department of Civil Engineering
College of Engineering
University of Wyoming
Research Project Technical
Completion Report (A-036-WYO)
Agreement No. 14-34-0001-2154
Prepared for:
U. S. Department of the Interior
The research on which this report is based was financed
in part by the U. S. Department of the Interior, as authorized
by the Water Research and Development Act of 1978 (P.L. 95-467).
Contents of this publication do not necessarily reflect
the views and policies of the U.S. Department of the Interior,
nor does mention of trade names or commercial products
constitute their endorsement or recommendation for use by the
U. S. Government.
Wyoming Water Research Center
University of Wyoming
Laramie, Wyoming
INTRODUCTION
The design of hydraulic structures for use in ungaged drainage basins requires some estimate of flood flows and their frequency of occurrence. Because no historical streamflow data exist for these drainages, floods are estimated either by regional frequency analysis or, with the help of digital computers, by parametric rainfall-runoff event simulation.Computer models dealing with rainfall-runoff event simulation are commonly used today by engineers and hydrologists. These models are used to predict flood hydrographs given an input rainfall volume, distributed over time in some manner, and certain geomorphic basin parameters.
Studies exist in the literature documenting the effects of time distribution of rainfall on runoff hydrographs. The reader is referred to works by Wei and Larson (1971), Yen and Chow (1980), and Shanholtz and Dickerson (1964) as examples. Because this relationship between the time distribution of rainfall and hydrograph characteristics exists, the separate study of storm rainfall is essential for accurate flood prediction regardless of other variables that also influence the runoff process. Additionally, methods of constructing design storms are available and in wide use, but they are general in nature and assume storms occur with the same temporal distribution across much of the country. Because of the drastic climatic differences between the areas encompassed by existing procedures, it was felt their design curves are not likely to be representative of the actual time distribution of storms in semi-arid regions such as Wyoming. It was, therefore, decided to develop a new design storm construction procedure applicable to the State of Wyoming based on observed storm rainfall in Wyoming. This new design storm methodology is the topic addressed herein.
REVIEW OF PREVIOUS WORK
Relatively few precipitation studies made to date deal with the temporal distribution of rainfall as used by hydrologists and engineers in parametric flood prediction.The Soil Conservation Service (SCS) method (1973) presents two temporal rainfall distribution curves for runoff prediction. For studies in Hawaii, Alaska, and the coastal side of the Sierra Nevada and Cascade mountain ranges, the Type I and IA curves are used. The Type II curve is applied in the remaining part of the United States, Puerto Rico, and the Virgin Islands. These curves are based on generalized rainfall depth- duration curves obtained from published data of the U.S. Weather Bureau (National Oceanic and Atmospheric Administration). All design storms developed with this method, regardless of duration, are based on the 24-hour volume for a given frequency and location.
The Bureau of Reclamation method (1977) is developed in two parts, one for the United States east of the 105° meridian and the other for areas west of the 105° meridian. The procedure requires arranging hourly rainfall increments in a specified sequence depending on the duration and type of storm (thunderstorm or general storm). Maximum 6-hour point rainfall values are used in designing general storms, and maximum 1-hour point rainfall values are used in designing thunderstorms.
The U.S. Weather Bureau procedure (1961) uses depth-duration-frequency (DDF) curves in design storm construction. In this method rainfall intensities are obtained from the DDF curves for a given frequency and duration at a certain locality. These intensities are then rearranged arbitrarily to form a storm pattern.
Kerr, et al., (1974) present a method of hyetograph construction for the State of Pennsylvania. Cumulative dimensionless rainfall versus time graphs used by the method are derived from historical rainfall data. The curves allow the user much flexibility because, rather than define a single storm sequence, they bracket a range of possible storm patterns. Picking the time distribution of a design storm is up to the user, providing he stays within the limits of the bracketing curves and the minimum and maximum intensities given.
Huff (1967) presents a procedure derived from heavy storms observed in Illinois. His distribution patterns are based on the time quartile in which the majority of rain occurs for a given storm. For each quartile storm type, frequency values are given so that the user knows the return period of his design storm.
A method described in Keifer and Chu (1957) uses intensity-duration- frequency curves for hyetograph design at a given location. In general, the proposed storm pattern is fit to exponential growth and decay curves with the most intense part of the storm defined by a parameter termed the "advanceness ratio." This method was developed in Chicago for urban sewer design but can easily be used in other areas of the country where adequate rainfall records are available.
Frederick, et al. (1981) developed annual maximum precipitation events for different durations. The largest precipitation amounts for the selected durations which coincide with a given duration event are selected. The events are stratified according to magnitude and ratios of shorter to longer duration precipitation totals are formed. Accumulated probabilities of this ratio are suggested as a tool to estimate precipitation increments necessary in the synthesis of precipitation mass curves. By analyzing the relative timing of the shorter duration event within the longer duration event, a characteristic time distribution can be developed.
METHODOLOGY
Accumulation of Rainfall DataThe definition of a storm had to be established before usable information could be obtained from the data. In this report, the criteria used for defining a storm are as follows:
General Storm - preceded and followed by at least two hours of
zero rainfall
TABLE I.
PRECIPITATION STATIONS PROVIDING DATA FOR STUDY
___________________________________________________________________
Reference Location Name or Major Drainage Recording
Number Number Basin Source Interval
1 Casper WSO AP North Platte NOAA1 Hourly
2 Cheyenne WSFO AP North Platte NOAA Hourly
3 Douglas Aviation North Platte NOAA HOURLY
4 Encampment North Platte NOAA Hourly
5 Jelm North Platte NOAA Hourly
6 Laramie 2 WSW North Platte NOAA Hourly
7 Medicine Bow North Platte NOAA Hourly
8 Oregon Trail Crossing North Platte NOAA Hourly
9 Pathfinder Dam North Platte NOAA Hourly
10 Phillips North Platte NOAA Hourly
11 Pine Bluffs North Platte NOAA Hourly
12 Rawlins FAA AP North Platte NOAA Hourly
13 Saratoga 4 N North Platte NOAA Hourly
14 Seminoe Dam North Platte NOAA Hourly
15 Shirley Basin Station North Platte NOAA Hourly
16 Torrington 1 S North Platte NOAA Hourly
17 Wheatland 4 N North Platte NOAA Hourly
18 Buffalo Powder NOAA Hourly
19 Douglas 17 NE Powder NOAA Hourly
20 Dull Center Powder NOAA Hourly
21 Gillette 18 SW Powder NOAA Hourly
22 Hat Creek 14 N Powder NOAA Hourly
23 Lance Creek Powder NOAA Hourly
24 Moorcroft Powder NOAA Hourly
25 Mule Creek Powder NOAA Hourly
26 Newcastle Powder NOAA Hourly
27 Osage Powder NOAA Hourly
28 Pine Tree 9 NE Powder NOAA Hourly
29 Powder River Powder NOAA Hourly
30 Recluse Powder NOAA Hourly
31 Sheridan WSO AP Powder NOAA Hourly
32 Story Powder NOAA Hourly
33 Boysen Dam Big Horn NOAA Hourly
34 Lander WSO AP Big Horn NOAA Hourly
35 Meteetse 1 ESE Big Horn NOAA Hourly
36 Powell Field Station Big Horn NOAA Hourly
37 Riverton Big Horn NOAA Hourly
38 Tensleep 4 NE Big Horn NOAA Hourly
39 Thermopolis Big Horn NOAA Hourly
40 Thermopolis 25 WNW Big Horn NOAA Hourly
41 Worland Big Horn NOAA Hourly
42 Big Piney Green NOAA Hourly
43 Mountain View Green NOAA Hourl
TABLE I. continued
PRECIPITATION STATIONS PROVIDING DATA FOR STUDY
___________________________________________________________________
Reference Location Name or Major Drainage Recording
Number Number Basin Source Interval
44 Mud Springs Green NOAA Hourly
45 Rock Springs FAA AP Green NOAA Hourly
46 Lake Yellowstone Yellowstone NOAA Hourly
47 Jackson Snake NOAA Hourly
48 Moran 5 WNW Snake NOAA Hourly
49 Evanston 1 E Bear NOAA Hourly
50 06631150 North Platte USGS2 5-minutely
51 06634910 North Platte USGS 5-minutely
52 06634950 North Platte USGS 5-minutely
53 06644840 North Platte USGS 5-minutely
54 06648720 North Platte USGS 5-minutely
55 06648780 North Platte USGS 5-minutely
56 06312910 Powder USGS 5-minutely
57 06312920 Powder USGS 5-minutely
58 06313050 Powder USGS 5-minutely
59 06313180 Powder USGS 5-minutely
60 06316480 Powder USGS 5-minutely
61 06382200 Powder USGS 5-minutely
62 06233360 Big Horn USGS 5-minutely
63 06238760 Big Horn USGS 5-minutely
64 06238780 Big Horn USGS 5-minutely
65 06256670 Big Horn USGS 5-minutely
66 06267260 Big Horn USGS 5-minutely
67 06267270 Big Horn USGS 5-minutely
68 06274190 Big Horn USGS 5-minutely
______________________________________________________________________
1 NOAA (1948-1979)
2 Rankl and Barker (1977)
=====================================================================
- at least four hours in duration
- at least one. half (0.5) inch in volume
Thunderstorm - preceded and followed by at least one hour of
zero rainfall
- at least twenty minutes and at most four hours
in duration
- at least one-half (0.5) inch in volume
These criteria are arbitrary but consistent with similar criteria put
forth by Huff (1967), Ward (1973), and Croft and Marston (1950). Minimum
duration requirements were used to make sure the time distribution of any
storm was described by at least four data points. In all, 531 general
storms and 72 thunderstorms were examined.
The period of record represented by the data at most stations covers the years 1969-1979, though the lack of definable storms at some stations required data from as far back as 1948. Because the development of design storms inherently assumes future rainfall events will occur with the same distribution as past events, the use of data from stations with variable periods of record is acceptable.
Description of Study Areas
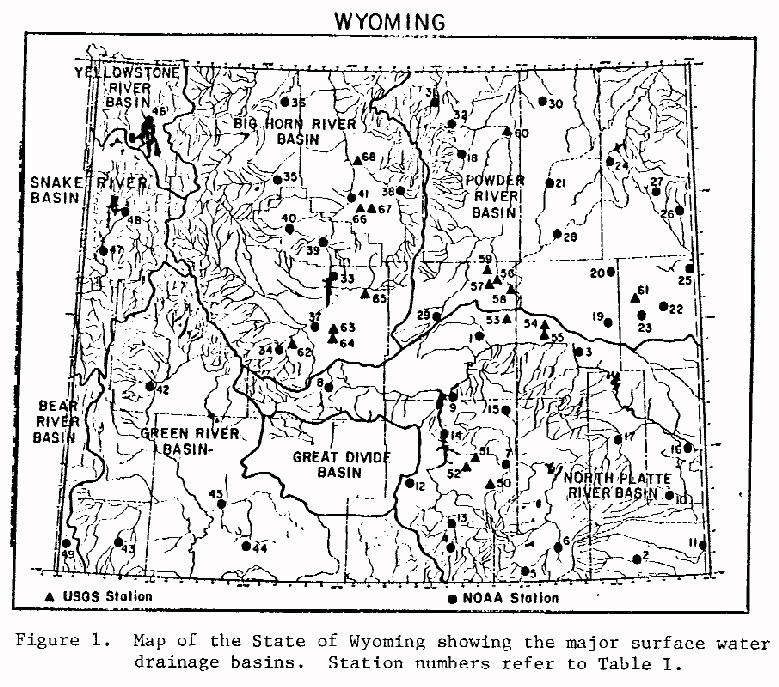
The State of Wyoming was divided into its major surface water drainage
basins for this study. This was done to see if differences in storm
rainfall characteristics exist between basins. Figure 1 shows the entire
State of Wyoming divided into these major drainages.
Analysis of Storm Parameters
Determining if differences in storm rainfall characteristics exist
between basins requires statistical analysis of certain storm parameters.
Definitions of parameters used in describing storm rainfall follow:
Storm Duration - the amount of elapsed time, in hours, from the
beginning to the end of a storm.
Storm Volume - the total amount of rainfall measured during a
storm, in inches.
Storm Intensity - the average rainfall rate during a storm, in inches
per hour, calculated by dividing a storm's volume
by its duration.
Percent Time to Peak Intensity - that amount of time, expressed as a
percent of total storm duration, from the beginning
of a storm to the period of most intense rainfall.
Pattern Index - the area beneath a dimensionless cumulative rainfall
versus time curve, expressed as a decimal or as a
percent.
Pattern Index and Percent Time to Peak Intensity were the parameters
used for determining if differences in the time distribution of rainfall
exist between basins. This determination was made using a one-way analysis
of variance technique for samples of unequal size. The procedure,
described in Miller and Freund (1977), tests for differences in the
population means for the populations from which the samples were taken.
Such tests indicate if significant differences in parameter values exist
between all the major drainages. If differences existed, the state would
have to be divided accordingly before design storms could be constructed.
If no differences existed, the state as a whole could be analyzed with the
resulting design storms applicable statewide.
Construction of Design Curves
All the observed dimensionless mass rainfall curves are superimposed
on one graph to create a family of "probable" storm patterns. Such an
approach to design storm development is described in Kerr, et al. (1974).
The method's most attractive feature is its flexibility, allowing the user
his choice of three given design hyetographs, as well as the freedom to
construct his own hyetograph, within limits. Such flexibility is desirable
when, for example, a person is designing a structure based on peak flowrate
in one instance and on runoff volume in another. The use of several curves
can allow maximization of either peak flowrate or runoff volume for a
given storm volume. A single design curve does not have this ability.
Figure 2 is a set of design curves. All of the storms used in the development: of this set of curves are non-dimensionalized and plotted on one graph of percent rainfall versus percent time. The bold vertical lines at each ten percent time increment represent the range of all storm data used. In the center of the plot is the mean curve. The curve is fit through the points representing the average cumulative percent rainfall at each ten percent time increment. It should be noted that the mean curve does not describe the average observed storm, rather it shows average accumulated rainfall with time based on all storms used. Also drawn on the plot: are ten percent and 90 percent limit curves. The ten percent limit curve represents, at a given percentage of storm duration, that value above which ten percent of the storms had accumulated more precipitation. Similarly, ten percent of the storms had each accumulated less than the value described by the 90 percent limit line at a given percentage of storm duration. It is not correct to assume that ten percent of the storms were totally above the ten percent limit line or totally below the 90 percent limit line. The use of ten percent as the cutoff when defining the upper and lower limit lines is arbitrary but reasonable. Using a smaller cutoff percentage resulting in a broader set of enveloping limit curves would be too general to accurately predict probable storm patterns. A larger cutoff value would result in a narrower envelope and a loss in flexibility of the method.
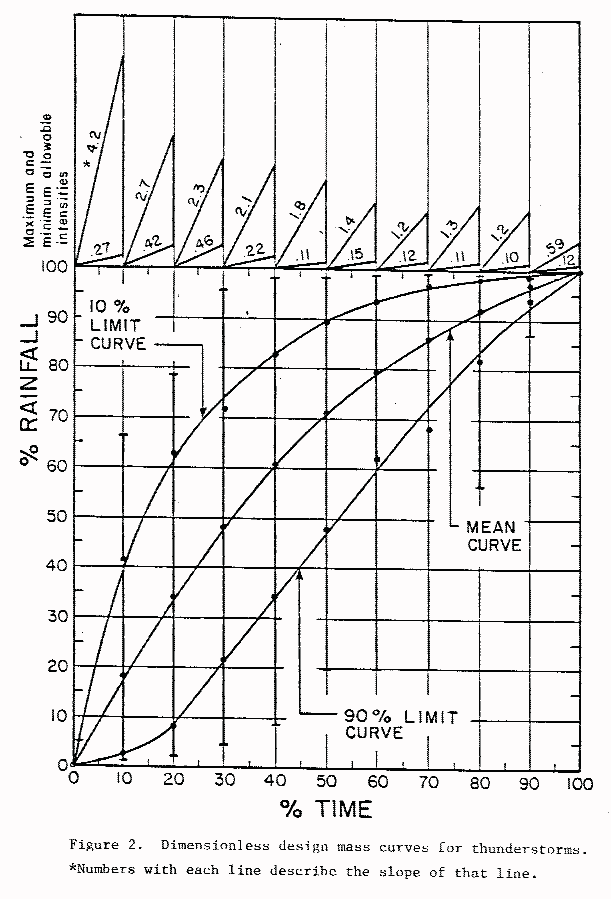
Under the assumption that future rainfall events will have the same time distribution as past events, these limit curves are the boundaries of a region of probable storm sequences. The user of the curves has the freedom to use either limit curve, or the mean curve, when choosing a design storm. In fact, he may pick his own storm sequence as long as he stays between the limit curves at all times and adheres to the maximum and minimum slope guidelines printed at the top of Figure 2. These guidelines are constructed in a manner similar to the limit curves in that for each ten percent time interval they represent intensities exceeded by ten percent of the storms (the steeper line) as well as intensities exceeded in 90 percent of the storms (the less steep line). In using these intensity guidelines, the designer cannot create a storm with an intensity greater than the value defined by the steep line or less than that defined by the shallow line for the appropriate ten percent increment of storm duration. The number accompanying each of these lines at the top of Figure 2 is the slope of that line.
Designing storms in this manner makes the utmost use of historical rainfall patterns while allowing the user flexibility in choosing the time distribution which will provide the critical peak flowrate or runoff volume for his purpose.
Comparison of Storm Design Methods
The creation of new storm patterns for use in a particular region is
logically accompanied by a comparison of the results of using the new
method with results obtained using established design storm techniques.
Such a comparison will prove the need for the new region-specific design
curves if the existing general methods do not produce similar runoff
characteristics when applied to a given event.
The different storm designs are compared by inputting them to four different rainfall-runoff simulation models and examining the runoff hydrographs produced. Thunderstorm and general storm runoff are simulated with each model. For each model and storm type the infiltration parameters are held constant so that any differences noted in outflow hydrograph characteristics can be attributed to differences in the input hyetographs. The models used are described in Table II. In addition to the design storm construction method presented in this paper, techniques given by the U.S. Soil Conservation Service (1973) and the U.S. Bureau of Reclamation (1977) are used for comparative purposes. These last two methods have already been described in the review of previous work.
DESIGN STORM RESULTS
Statistical Analysis
TABLE II
DESCRIPTION OF DIGITAL COMPUTER MODELS USED IN DESIGN STORM COMPARISONS
=======================================================================================================
Method of estimating Method of constructing
Model Citation infiltration outflow hydrograph
_______________________________________________________________________________________________________
SCS Triagular U.S. Soil Conser- Uses a "minimum infiltration Relates incremental excess
Hydrograph vation Service rate" and runoff curve num- precipitation to incremental
(1972). ber based on soil type. runoff with a hydrograph
that is triangular in shape.
HEC-1 U.S. Army Corps Uses an exponentially decay- Derives outflow hydrograph
of Engineers ing function that depends on from either (1) unitgraph
(1973). rainfall intensity and ante- input by either, or (2) Clark
cedent losses. (1945) synthetic unitgraph.
HYMO Williams and Hann Similar to SCS method Uses dimensionless unitgraph
(1973). U.S. De- above; uses curve number and (described by exponential
partment of Agri- minimum infiltration rate. expressions relating flowrate
culture. to time) and a "dimensionless
shape parameter."
USGS Dawdy, David R., Uses the Philip (1954) var- Performs finite difference
John C. Shaake, Jr.,iation of the Green-Ampt solution of kinematic wave
and William M. (1911) equation. Method in- equation for each channel and
Alley (1978). cludes soil-moisture account- overland flow segment in drain-
U.S. Geological ing between storms. age basin.
Survey.
=======================================================================================================
Inferred by 1 and 2 above is the need for only one set of general
storm design curves and one set of thunderstorm design curves for use
statewide. Conclusion 3 says that design storms of varying duration, i.e.,
1-, 2-, or 3-hour thunderstorms or 6-, 12-, or 24-hour general storms, can
all be handled with the same set of design curves. Table III lists the
results of selected important linear regression and ANOVA tests used in
drawing these conclusions. The rest of the statistical analysis results
can be found in Tyrrell (1982).
Probably the most outstanding characteristic of the storms analyzed is their individual diversity. This same finding is corroborated in the paper by Kerr, et al. (1974) for storms in Pennsylvania. It is precisely because of this diversity that the use of an enveloping set of curves is preferred to the use of a single storm pattern when attempting to predict runoff. Presentation and Use of Design Curves
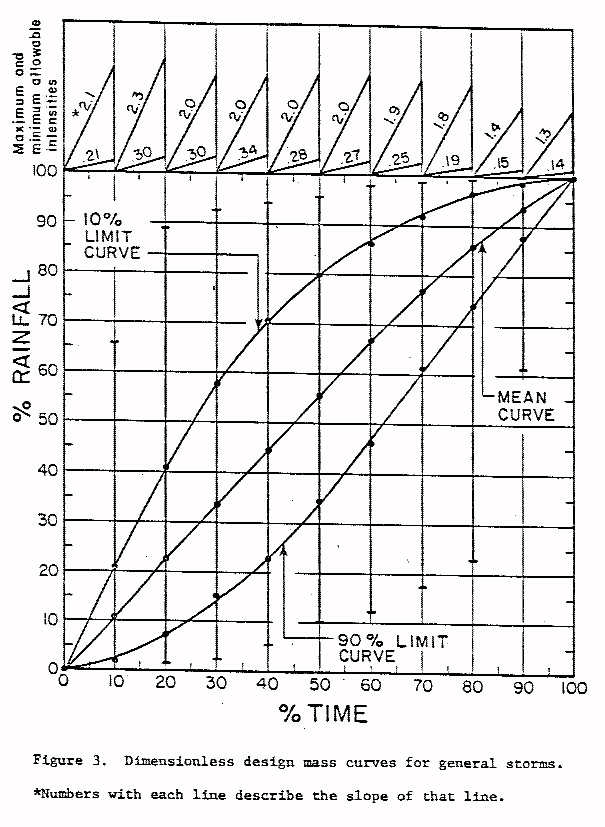
Figures 2 and 3 are the design curves for thunderstorms and general storms, respectively, constructed according to the procedures outlined previously. Figure 2 is to be used when the duration of the design storm of interest is less than four hours. Figure 3 is used for events four hours long or longer.
TABLE III
RESULTS OF SELECTED STATISTICAL ANALYSIS OF RAINFALL CHARACTERISTICS
======================================================================================================
Linear Regression
______________________________________________________________________________________________________
Correlation
Dependent Variable vs Independent Variable Coefficient(R) Conclusion
Pattern Index for all Duration of all storms. .167 No significant relationship.
storms.
*Duration of all general Percent time to Peak In- .055 No significant relationship.
storms-North Platte tensity-general storms-
drainage. North Platte drainage.
*Duration of all thunder- Percent time to Peak In- .170 No significant relationship.
storms-North Platte tensity-thunderstorms-
drainage. North Platte drainage.
______________________________________________________________________________________________________
TABLE III, continued
RESULTS OF SELECTED STATISTICAL ANALYSIS OF RAINFALL CHARACTERISTICS
======================================================================================================
Analysis of Variance
______________________________________________________________________________________________________
Null Hypothesis (Ho) F Statistic Conclusion
Data F.05 F.10 _______________________________________
Pattern Index values for general 1.22 2.44 1.99 Do not reject Ho; conclude no difference
storms are equal for all five in Pattern Index due to drainage basin
major drainages. location.
Pattern Index values for thunder- .79 3.14 2.38 Do not reject Ho; conclude no difference
storms are equal for three in Pattern Index due to drainage basin
major drainages. location.
*Pattern Index values are equal for 24.65 3.91 2.74 Reject Ho; conclude some difference in
thunderstorms and general storms- Pattern Index due to type of storm.
North Platte River drainage.
_______________________________________________________________________________________________________
*Results from the North Platte drainage data analysis are presented as an example. Results from the
other basins are similar.
======================================================================================================
Following is a list of steps involved in using the design curves:
TABLE IV
RECOMMENDED TIME INTERVALS AND CORRESPONDING PERCENT
TIME INCREMENTS FOR OBTAINING RAINFALL VERSUS
TIME DATA FROM DESIGN CURVES
=====================================================================
Interval as a
Storm Recommended Number of Percent of
Duration Time Interval Intervals Storm Duration
30 minute 5 minute 6 16.67%
1 hour 10 minute 6 16.67%
2 hour 15 minute 8 12.50%
3 hour 15 minute 12 8.33%
6 hour 30 minute 12 8.33%
12 hour 1 hour 12 8.33%
24 hour 1 hour 24 4.17%
=====================================================================
It is recommended that the user run several simulations with different
hyetographs to determine the critical runoff volume or peak flowrate. The
suite of design curves used probably will include both limit curves, the
mean curve, and several curves chosen arbitrarily by the user.
A parameter not included in this study is the areal distribution of rainfall. Therefore, the user of the method presented here is obliged to reduce point rainfall values when working with large drainage basins. Methods of reducing point rainfall with increasing drainage basin area are presented in Design of Small Dams (U.S. Bureau of Reclamation, 1977) and in the Rainfall Frequency Atlas (Miller, et al., 1973). These reductions are necessary because of the tendency of point rainfall values to overestimate actual areal precipitation on large areas.
Because this new design method depicts "probable" events, rather than extreme events (i.e., ultra-high-intensity bursts or long periods of very intense rain), it should not be used when designing for runoff due to "probable maximum" rainfall. Existing methods for probable maximum design (as in Small Dams) should be consulted for those cases.
RESULTS OF DESIGN STORM COMPARISONS
General InformationThe procedure followed in the comparison was to input differing design storms to a model, while leaving all geomorphic and loss parameters unchanged, and examine differences in the simulated outflow hydrograph peak and volume. Variations thus found are attributable to variations in the input hyetograph.
Some problems were encountered in the use of existing design storms. For example, the SCS method, rather than using a rainfall volume based on a certain duration for a given frequency, uses the 24-hour amount for designing storms of all durations. This practice results in slightly different storm volumes than those found in the Miller, et al. (1973), publication for varying durations. Despite this anomaly, the SCS hyetograph was used without a volume correction. Thus, a valid method-by-method comparison is ensured. The Bureau of Reclamation (BUREC) method also involves an odd twist basing its storm volumes on fractions and multiples of the 6-hour value for a given frequency. Modern practice has corrected this deficiency by allowing the use of volumes expected for various durations, not a manipulation of the 6-hour amount, while retaining the recommended time sequence. The BUREC method also typically calls for basing designs on runoff from a 3-hour thunderstorm and an 18-hour general storm. Because there exists no 18-hour duration precipitation data, no storms of this length were used in comparison. Also, a 2-hour thunderstorm was deemed most representative of short duration events (thus, the 3-hour event was not used).
Storms selected for the comparisons were 2, 6 and 24 hours in duration. The 2-hour event is considered a thunderstorm; the other two are general storms. A small drainage in the Powder River Basin provided the geomorphic data for the simulations. Storm volumes (U.S. Weather Bureau, 1961) for the duration's listed above (with a 1O-year return period) at this location are:
2-hour - 1.60"
6-hour - 2.00"
24-hour - 2.75"
while the geomorphic parameters for the basin are:
Drainage Area - 0.83 mi2
Water Course Length - 1.38 mi.
Elevation Difference - 125 feet
Model ParametersBecause all the results presented herein were obtained using non-calibrated infiltration parameters, they are useful for comparison purposes only.
TABLE V
LOSS PARAMETERS USED WITH RAINFALL RUNOFF MODELS
FOR STORM COMPARISON
==========================================================================
Mon. Infil-
Curve tration Rate
Model Number (in/hr) STRKR1 DRTKR1 RTIOL1 ERAIN1 TC1 R1
HYDRO 72 .15 NA NA NA NA NA NA
HYMO 72 .15 NA NA NA NA NA NA
HEC-1 NA NA .80 .20 2.75 .70 1.0 5.0
PSP* KSAT* RGI* BMSN* EVC* RR* DRN/(24˙KSAT)*
USGS 5.0 0.10 10.0 5.0 0.7 0.9 0.5
==========================================================================
*For definition of parameters refer to dawdy, et al. (1978).
1The reader is referred to the HEC-1 users manual (U.S. Army Corps of
Engineers, 1973) for definitions of these infiltration parameters.
Design Hyetographs
TABLE VI
COMPARATIVE HYETOGRAPHS FOR 10 YEAR, 2-HOUR THUNDERSTORM
Cumulative Rainfall (inches)
=====================================================================================================
Time, *SCS WYO: 10% 90%
Minutes Type II BUREC Mean Limit Limit A B C D E F G H
_____________________________________________________________________________________________________
0 ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
15 .06 .14 .35 .75 .06 .30 .67 .75 .35 .35 .30 .35 .35
30 .15 .36 .66 1.10 .24 .38 .77 1.02 .66 .66 .38 .58 .66
45 .45 .65 .91 1.30 .50 .50 .83 1.09 .91 .91 .50 .64 .80
60 1.17 1.26 1.14 1.44 .75 .83 .85 1.12 .98 1.14 .75 .75 .82
75 1.30 1.39 1.30 1.50 1.01 1.10 1.01 1.15 1.01 1.17 1.01 1.01 1.01
90 1.37 1.49 1.42 1.55 1.25 1.34 1.25 1.25 1.25 1.25 1.25 1.25 1.25
105 1.43 1.55 1.52 1.58 1.44 1.57 1.44 1.44 1.44 1.44 1.44 1.44 1.44
120 1.47 1.60 1.60 1.60 1.60 1.60 1.60 1.60 1.60 1.60 1.60 1.60 1.60
_____________________________________________________________________________________________________
*Based on 10 year, 24-hour volume (2.75")
=====================================================================================================
TABLE VII
COMPARATIVE HYETOGRAPHS FOR 10 YEAR, 6-HOUR GENERAL STORM
Cumulative Rainfall (inches)
=====================================================================================================
Time, *SCS WYO: 10% 90%
Minutes Type II BUREC Mean Limit Limit C G
_____________________________________________________________________________________________________
0 ---- ---- ---- ---- ---- ---- ----
30 .04 .18 .34 .04 .04 .34
60 .10 .14 .36 .68 .10 .10 .68
90 .17 .56 1.00 .22 .36 .84
120 .24 .32 .74 1.24 .34 .68 .88
150 .41 .92 1.44 .50 1.00 .94
180 1.41 .54 1.12 1.60 .68 1.34 .98
210 1.62 1.30 1.72 .90 1.68 1.04
240 1.72 1.50 1.46 1.82 1.12 1.82 1.12
170 1.80 1.64 1.88 1.34 1.88 1.34
300 1.86 1.82 1.76 1.94 1.56 1.94 1.56
330 1.92 1.90 1.98 1.78 1.98 1.78
360 1.96 2.00 2.00 2.00 2.00 2.00 2.00
_____________________________________________________________________________________________________
*Based on 10 year, 24-hour volume (2.75")
=====================================================================================================
TABLE VIII
COMPARATIVE HYETOGRAPHS FOR 10 YEAR, 24-HOUR GENERAL STORM
Cumulative Rainfall (inches)
=====================================================================================================
Time, SCS WYO: 10% 90%
hours Type II BUREC Mean Limit Limit A B C D E F G H
_____________________________________________________________________________________________________
0 --- --- --- --- --- ---- ---- ---- ---- ---- ---- ---- ----
1 .03 .05 .11 .22 .03 .03 .03 .03 .03 .22 .22 .22 .22
2 .06 .14 .25 .47 .06 .06 .06 .06 .06 .47 .47 .47 .47
3 .09 .22 .36 .72 .08 .08 .08 .08 .08 .72 .72 .72 .61
4 .13 .33 .50 .94 .14 .14 .14 .14 .14 .94 .94 .94 .63
5 .17 .44 .66 1.16 .22 .22 .22 .25 .22 1.16 1.16 1.10 .66
6 .22 .55 .77 1.38 .30 .30 .30 .50 .30 1.38 1.38 1.16 .72
7 .28 .66 .91 1.54 .39 .39 .39 .72 .39 1.54 1.54 1.18 .74
8 .34 .80 1.02 1.71 .47 .47 .58 .94 .47 1.71 1.60 1.21 .77
9 .41 .96 1.16 1.84 .58 .58 .80 1.18 .58 1.84 1.65 1.27 .83
10 .51 1.71 1.27 1.98 .69 .74 1.02 1.38 .69 1.93 1.68 1.29 .85
11 .65 1.95 1.40 2.09 .80 .96 1.27 1.62 .80 1.98 1.71 1.32 .88
12 1.82 2.09 1.54 2.20 .94 1.18 1.49 1.84 .94 2.01 1.73 1.35 .94
13 2.13 2.15 1.65 2.28 1.07 1.40 1.71 2.06 1.18 2.04 1.76 1.38 1.07
14 2.26 2.20 1.79 2.37 1.24 1.62 1.93 2.31 1.40 2.06 1.79 1.43 1.24
15 2.34 2.25 1.90 2.45 1.38 1.84 2.15 2.45 1.62 2.09 1.84 1.49 1.38
16 2.42 2.31 2.01 2.50 1.54 2.09 2.37 2.50 1.84 2.12 1.87 1.54 1.54
TABLE VIII continued
COMPARATIVE HYETOGRAPHS FOR 10 YEAR, 24-HOUR GENERAL STORM
Cumulative Rainfall (inches)
=====================================================================================================
Time, SCS WYO: 10% 90%
hours Type II BUREC Mean Limit Limit A B C D E F G H
_____________________________________________________________________________________________________
17 2.48 2.37 2.12 2.53 1.68 2.28 2.53 2.53 2.06 2.15 1.90 1.68 1.68
18 2.54 2.42 2.26 2.59 1.84 2.50 2.59 2.59 2.26 2.17 1.90 1.84 1.84
19 2.58 2.47 2.34 2.64 2.01 2.64 2.64 2.64 2.48 2.20 2.01 2.01 2.01
20 2.62 2.53 2.42 2.67 2.15 2.67 2.67 2.67 2.64 2.20 2.15 2.15 2.15
21 2.66 2.59 2.53 2.70 2.28 2.70 2.70 2.70 2.70 2.28 2.28 2.28 2.28
22 2.70 2.64 2.61 2.72 2.45 2.72 2.72 2.72 2.72 2.45 2.45 2.45 2.45
23 2.72 2.69 2.67 2.72 2.59 2.72 2.72 2.72 2.72 2.59 2.59 2.59 2.59
24 2.75 2.75 2.75 2.75 2.75 2.75 2.75 2.75 2.75 2.75 2.75 2.75 2.75
_____________________________________________________________________________________________________
=====================================================================================================
visually with the standard 10%, 90% and mean WYO curves. The reader can
see that, due to the discrepancy previously described, the SCS storm
volumes do not quite equal the volumes given by the BUREC and WYO storms in
Tables VI and VII.
The 6-hour event was the last of the three to be evaluated. Results from the earlier runs for the 2- and 24-hour events were used to indicate which of the lettered (A, B, C, etc.) WYO curves would probably give the largest peak runoff flowrate. As a result, the 6-hour event was run with only the "C" and "G" arbitrary curves used in addition to the mean, ten percent limit, and 90 percent limit curves.
Tables IX, X, and XI present the results of the model runs for the 2-hour, 6-hour and 24-hour events, respectively. Generally, results from HEC-1, HYMO, and HYDRO simulations show that for longer events the WYO curves produce less runoff (Peak and Volume) than the other methods, while for shorter events the WYO curves produce greater runoff. Results from USGS model runs differed from the other models* results by predicting, for all three storm durations, smaller runoff peaks and volumes due to the WYO design curves when compared to established procedures. Because of these results, it is suggested that current methods may lead to consistent over- design of hydraulic structures, at least when long (durations of 6 or more hours) events are stated as part of the design criteria. Also, the ability of any one of the group of WYO curves to produce greater runoff than the others is dependent upon the model used. These results are further detailed in the following section.
TABLE IX
RUNOFF CHARACTERISTICS FOR 10 YEAR 2-HOUR THUNDERSTORM
========================================================================
MODEL:
HYDRO HYMO HEC-1 USGS____
Peak Vol. Peak Vol. Peak Vol. Peak Vol.
Design Storm (cfs) (in.) (cfs)(in.) (cfs)(in.) (cfs) (in.)
_________________________________________________________________________
SCS Type II 47.8 .098 11.7 .036 38 .39 41.1 .162
BUREC 65.3 .137 17.3 .053 36 .38 40.2 .162
WYO-Mean 61.7 .139 12.9 .040 28 .31 16.0 .094
10% Limit 61.8 .123 19.9 .061 42 .45 33.2 .146
90% Limit 76.1 .135 30.7 .100 29 .32 20.6 .107
-A 79.6 .134 41.7 .133 31 .34 24.7 .118
-B 75.3 .133 30.9 .100 32 .39 23.1 .124
-C 62.2 .124 17.2 .064 34 .42 22.2 .138
-D 72.6 .132 30.7 .100 29 .35 19.3 .105
-E 62.5 .130 21.0 0.80 28 .34 18.0 .102
-F 76.1 .135 30.7 .100 27 .31 19.9 .105
-G 76.1 .135 30.7 .100 27 .32 19.2 .103
-H 76.7 .134 30.7 .100 28 .33 18.9 .103
========================================================================
TABLE X
RUNOFF CHARACTERISTICS FOR 10 YEAR 6-HOUR GENERAL STORM
========================================================================
MODEL:
HYDRO HYMO HEC-1 USGS____
Peak Vol. Peak Vol. Peak Vol. Peak Vol.
Design Storm (cfs) (in.) (cfs)(in.) (cfs)(in.) (cfs) (in.)
_________________________________________________________________________
SCS Type II 85.3 .175 42.7 .143 36 .38 47.1 .184
BUREC 81.6 .251 37.6 .205 20 .23 19.4 .116
WYO-Mean 52.8 .275 18.9 .094 2 .03 6.7 .065
10% Limit 50.5 .208 26.9 .103 11 .14 8.5 .075
90% Limit 83.6 .287 54.8 .261 10 .12 12.4 .085
-C 89.1 .221 49.4 .164 18 .22 16.7 .101
-G 83.6 .226 55.8 .261 10 .16 10.5 .082
========================================================================
TABLE XI
RUNOFF CHARACTERISTICS FOR 10 YEAR 24-HOUR THUNDERSTORM
========================================================================
MODEL:
HYDRO HYMO HEC-1 USGS____
Peak Vol. Peak Vol. Peak Vol. Peak Vol.
Design Storm (cfs) (in.) (cfs)(in.) (cfs)(in.) (cfs) (in.)
=========================================================================
SCS Type II 138.6 .346 57.9 .285 30 .34 43.1 .189
BUREC 95.5 .268 45.9 .221 14 .16 14.4 .103
WYO-Mean 0 0 0 0 0 0 1.49 .043
10% Limit 24.3 .107 14.7 .091 0 0 2.22 .051
90% Limit 8.0 .085 6.5 .074 0 0 2.88 .056
-A 50.9 .428 35.5 .352 0 0 5.16 .072
-B 37.6 .400 29.0 .327 0 0 4.91 .070
-C 50.9 .384 36.6 .319 0 0 5.18 .069
-D 37.6 .412 27.7 .343 0 0 4.94 .071
-E 24.3 .134 1.7 .005 0 0 2.22 .057
-F 24.3 .120 14.7 .099 0 0 2.31 .057
-G 8.1 .075 6.1 .063 0 0 2.82 .056
-H 8.1 .085 6.5 .074 0 0 2.88 .056
=======================================================================
DISCUSSION OF RESULTS
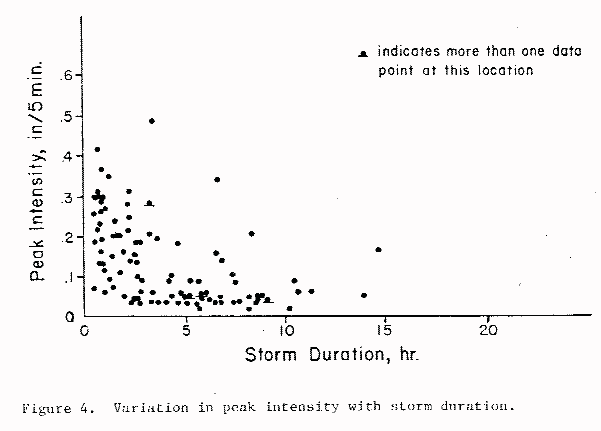
The most significant difference between the WYO design storm methodology and those developed by the Soil Conservation Service and Bureau of Reclamation is the use of totally dimensionless curves. By non- dimensionalizing the time axis, the average intensities of designed storms is decreased as the storm durations are increased. For example, if two general storms of the same volume but differing durations, say 6 hours and 12 hours, were distributed over time according to the mean curve of Figure 3, the 12-hour storm would have half the intensity of the 6-hour event at any point along the curve. This explains why the WYO curves tend to produce smaller runoff peaks than the other methods for long events, and larger peaks for short events. Such a change in intensity with duration may seem inappropriate at first, but analysis of one hundred runoff- producing storms recorded by Ranki and Barker (1977) shows that, while there is not a good linear relationship (R = 53%), the peak intensity of a storm appears to decrease with increasing storm length. Figure 4 suggests this graphically. It, therefore, seems reasonable for the WYU storm design technique to make long storms generally less intense than short storms.Lower rainfall intensity, as obtained from the WYO curves, is the reason zero runoff is predicted in some instances for the 24-hour event. For example, referring to Table XI, no runoff is produced using the WYO mean curve with the HYDRO and HYMO models. One will notice that, for general storms, the WYO mean curve is almost a 45░ line indicating an almost constant intensity storm. For the 24-hour event, this constant intensity (.11 in/hour) is less than the minimum infiltration loss of .15 in/hour. Thus, no runoff occurs. Similarly, the HEC-1 model produces zero runoff in several instances. Because shorter storms do produce runoff according to HEC-1, the reason for zero predicted runoff in the longer storms obviously also involves low rainfall intensity and associated infiltration losses.
It is interesting to note that choosing a WYO curve for producing peak runoff flowrate or volume depends on the computer model to be used. For instance, referring to Table IX, the WYO 90 percent limit curve produces more runoff (peak and volume) than the ten percent limit curve when HYDRO and HYMO are used. When HEC-1 is used, the ten percent limit curve yields the greatest runoff peak and volume. The user of these curves is, therefore, warned not to assume that a peak-producing hyetograph for one model will perform similarly with a different simulation scheme. Always test several curves for their peak-producing ability when changing models, or when changing storm durations with the same model.
SUMMARY AND CONCLUSIONS
SummaryComparisons were made between the WYO method and design storms recommended by the U.S. Soil Conservation Service and U.S. Bureau of Reclamation using HEC-1, HYMO, HYDRO (Triangular Hydrograph), and USGS Distributed Routing rainfall-runoff models.
Conclusions
REFERENCES
Clark, C. 0., 1945, Storage and the Unit Hydrograph, Am. Soc. Civil Engineers Trans., V. 110, pp. 1419-1488.Croft, A. R., and Richard B. Marston, 1950, Summer Rainfall Characteristics in Northern Utah, Trans. Am. Geophysical Union, Vol. 31, No. 1, pp. 83-95.
Dawdy, David R., John C. Schaake, Jr., and William M. Alley, 1978, Distributed Routing Rainfall-Runoff Model, U. S. Geological Survey, Water-Resources Investigations 78-90, 146 p.
Frederick, Ralph H., John F. Miller, Francis P. Richards and Richard W. W. Schwerdt, 1981, Interduration Precipitation Relations For Storms - Western United States, NOAA Technical Report NWS 27, U. S. Department of commerce, 195 pp.
Green, W. H. and G. A. Ampt, 1911, Studies on Soil Physics; I, Flow of Air and Water Through Soils: Jour. Agr. Research, V. 4, p. 1-24.
Haan, Charles T., and B. J. Barfield, 1978, Hydrology and Sedimentology of Surface Mined Lands, Lexington, Kentucky: University of Kentucky.
Haie, Nairn, 1980, Rainfall-Runoff Models for Ephemeral Streams in the Eastern Powder River Basin of Wyoming, M. S. Thesis, University of Wyoming, 56 pp.
Huff, F. A., 1967, Time Distribution of Rainfall in Heavy Storms, Water Resources Research 3(4):1007-1019.
Keifer, Clint J., and Henry Hsien Chu, 1957, Synthetic Storm Pattern for Drainage Design, Journal of the Hydraulics Division, ASCE, Vol. 83, No. HY4.
Kerr, R. L., T. M. Rachford, B. M. Reich, B. H. Lee, and K. H. Plummer, 1974, Time Distribution of Storm Rainfall in Pennsylvania, Pennsylvania State University, Institute for Research on Land and Water Resources, 34 pp.
Miller, Irwin, and John E. Freund, 1977, Probability and Statistics for Engineers, Second Ed. Prentice-Hall, Inc., Englewood Cliffs, New Jersey.
Miller, J. F., R. H. Frederick and R. J. Tracey, Precipitation-Frequency Atlas of the Western United States, Vol. II, Wyoming. NOAA Atlas 2. U. S. Dept. of Commerce, Silver Spring MD, 1973
National Oceanic and Atmospheric Administration (NOAA), 1948-1979, Hourly Precipitation Data for Wyoming, National Climatic Center Asheville, North Carolina.
Philip, J. R., 1954, An Infiltration Equation with Physical Significance: Soil Sci. Soc. Am. Proc., V. 77, p. 153-157.
Ranki, J. G., and D. S. Barker, 1977, Rainfall and Runoff Data from Small Basins in Wyoming, Wyoming Water Placing Program Report No. 17, 195 pp.
Shanholtz, V. 0., and W. H. Dickerson, 1964, Influence of Selected Rainfall Characteristics on Runoff Volume, West Virginia University Agricultural Experiment Station, Bulletin 4971.
Tyrrell, Patrick T., 1982,. Development of Design Rainfall Distribu- tion for the State of Wyoming, M. S. Thesis, University of Wyo- ming, 71 pp.
U. S. Army Corps of Engineers, 1973, HEC-1 Flood Hydrograph Package, Users and Programmers" Manuals, HEC Program 723-X6-L2010.
U. S. Bureau of Reclamation, 1977, Design of Small Dams, U. S. Dept. of the Interior, Washington, D.C.: U. S. Government Printing Office.
U. S. Soil Conservation Service, 1973, A Method for Estimating Volume and Rate of Runoff in Small Watersheds, SC-TP-149, Department of Agriculture.
U. S. Weather Bureau, 1961, Rainfall-Frequency Atlas of the United States for Durations from 30 Minutes to 24 Hours and Return Periods from 1 to 100 Years. Tech. Paper 40, 115 pp.
U. S. Weather Bureau, 1978, Use of DDF Curves in Storm Construction, In Hydrology and Sedimentology of Surface Mined Lands, Haan and Barfield (1978), pp. 49-52.
Ward, Tim, 1973, Quantification of Rainfall Characteristics, Unpublished. CWRR-DRI, University of Nevada System, Reno, Nevada.
Wei, Tseng C., and C. L. Larson, 1971, Effects of Areal and Time Distribution of Rainfall on Small Watershed Runoff Hydrographs, Minnesota Univ., Minneapolis, Water Resources Research Center, Bulletin No. 30, 130 pp.
Williams, J. R., and R. W. Hann, 1973, HYMO: Problem-Oriented Computer Language for Hydrologic Modeling, U. S. Department of Agriculture,Agriculture Research Service.
Yen, Ben Chie, and Ven Te Chow, 1980, Design Hyetographs for Small Drainage Structures, Journal of the Hydraulics Division, ASCE, Vol. 106.,No. HY6.
Water Resources Publications List
Water Resources Data System Library |
Water Resources Data System Homepage
| |||||||||||||||||||||||||||||||||||